2018/03/24 (2018年03月 のアーカイブ)
ステッピングモーターをいじっていて得た知見のメモ
せっかくなのでメモを残しておく。
話を簡単にするために、パルスを1つ送るとステッピングモーターのステップが1つ進む、という前提にしておく。
で、ステッピングモーターを1000ステップ回すためにはパルスを1000発送るわけだけど、モーターの特性として加減速レートの限界があり、急すぎる加速や急すぎる減速はできない。という事でゆっくりとスタートしてから加速して目的の速度に達すればそのまま維持、目的のステップ数に近づくと減速してから停止する、という処理が必要になる。
S字カーブみたいなのを使うと計算が面倒なので一般的に良く使われるのが台形制御。つまり下の図のような奴。
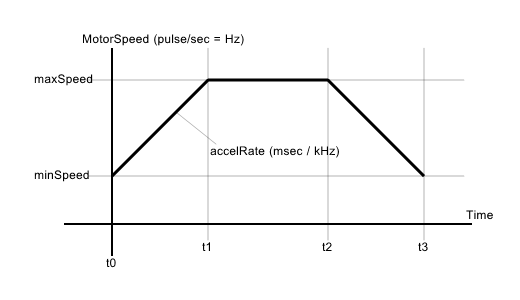
モーターの速度は秒間のパルス数、つまり周波数 \(Hz\) で表される。
\(minSpeed\) は静止状態との間で移行できる速度。\(accelRate\) は加速/減速の程度で速度が単位周波数変化するために必要な時間。単位は \(mSec / kHz\)、つまり \(uSec / Hz\)。 モーターが回転を開始すると \(minSpeed\) から一定の加速度で加速して目的の \(maxSpeed\) に達すると一定速度で運転、目的のステップ数が近づくと減速を開始し、目的のステップ数になった時にちょうど最低速度\(minSpeed\)になって停止する、という制御をしたい。
ここで問題なのがいつ減速を開始するか、つまり \(t2\) に到達したかの判定。
減速時、モーターに対して指示したステップ数の経過後に \(minSpeed\) に到達するため \(t2\) から \(t3\) 間に何ステップ進むかを知り、(総ステップ数 - 現在のステップ数) = 残りのステップ数 との比較で判定する必要がある。
という事で、\(t2\) から \(t3\) の間のステップ数は、
\[ steps = \int_{t2}^{t3} speed(t) dt \] \[ = (t3 - t2) * (maxSpeed + minSpeed) / 2 \]
また、 \[ t3 - t2 = (maxSpeed - minSpeed) * \frac{accelRate}{1000000} \] なので \[ steps = (maxSpeed - minSpeed) * (maxSpeed + minSpeed) * accelRate / 1000000 / 2\] \[ = (maxSpeed^2 - minSpeed^2) * accelRate / 2000000 \] という事になる。
逆に、残りステップ数が \(step\) の時の速度は \[ speed = \sqrt{ \frac{step * 2000000}{accelRate} + minSpeed^2 } \] になるが、これを直接使うと平方根計算に時間を取られるので、現在の速度は差分で積算する。 ステップ毎に処理する場合の減速中の現在速度\(currentSpeed_{(Hz)}\)の変化は \[ currentSpeed_{n+1} = currentSpeed_n - \frac{1000000}{currentSpeed_n * accelRate} \]
浮動小数計算だと遅すぎるのでなんとかオーバーフローしないように誤魔化しながら整数演算するとして、\(currentSpeed\)等は少なくとも 24.8 形式程度の固定小数で扱わないと誤差が累積しすぎる。
これを基に結構真面目にチューニングした奴を 16MHz Arduino で動かしてパルス速度 8kHz くらいまで動く。計算の手を抜けばもう少し速くなるけど、どうやら今使っているモーターの方がついてこない (1/8 マイクロステップ) のでこの辺にしておく。
https://github.com/g200kg/arduino-stepping-motor
Posted by g200kg : 2018/03/24 02:57:37



