2018/03/29 (2018年03月 のアーカイブ)
ステッピングモーターの制御についてもう少しメモ
さて、ステッピングモーターの加減速についてもうちょっと追加でメモ
取りあえず計算が簡単な台形制御での 時間(T)-速度(V) の動きがこれ。
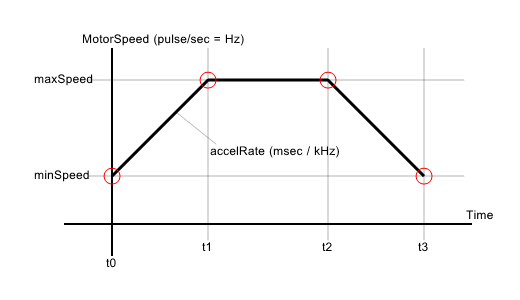
ここでの問題は加速度がステップ状になっていて不連続な点があり、そこで多少の衝撃が発生する事。なのでこの速度変化を滑らかにするのが S字制御である。こんな感じ↓
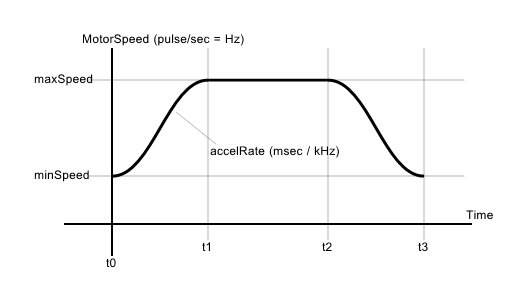
このカーブの作り方にも色々とやり方がありそう。
定石的に良く使われるのが三角関数での接続。
変化部分の時間経過を 0 < t < 1、min から max までの速度を 0 < v < 1 として、
\[
v = 0.5 - 0.5 cos( t \pi)
\]
テーブルを引いて処理するならこれで良いのだけど、一応リアルタイムに計算できそうなやり方も考える。負荷的に一番軽そうなのが、カーブの中心で上下を分けて上半分、下半分をそれぞれ二次曲線で接続するという方法
\[
\begin{eqnarray}
v =
\begin{cases}
t^2 & ( t \lt 0.5 ) \\
1 - (1 - t)^2 & ( t \geqq 0.5 )
\end{cases}
\end{eqnarray}
\]
あるいは三次曲線で一気に繋ぐという方が良いかも。
\[
v = -2 t^3 + 1.5 t + 0.5
\]
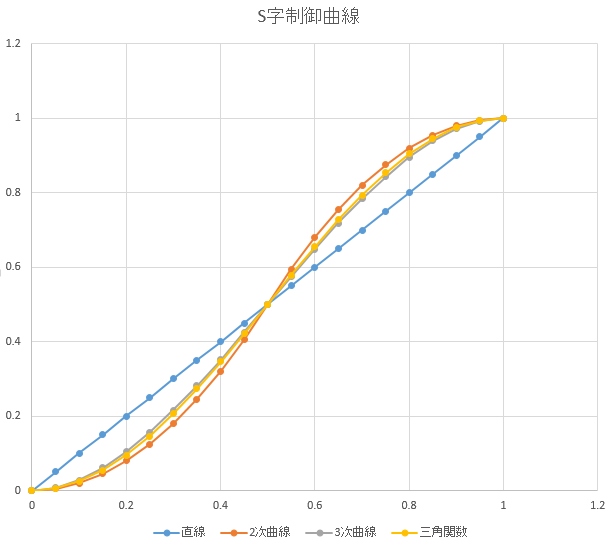
時間 - 速度のグラフで見てみるとこんな感じになる。
加速度の変化で見ると違いがわかりやすい
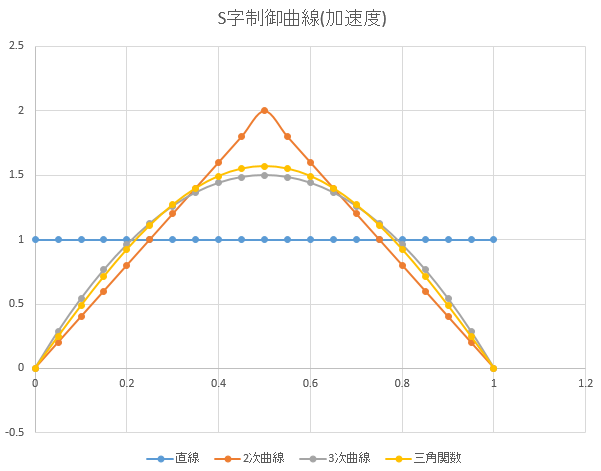
更に微分した加速度の変化、加加速度 = 躍度で言えば二次曲線でもカーブの繋ぎで不連続点がでる。
逆に三角関数接続と3次関数接続の違いはもうほとんどわからないのではないかな。というか実際にモーターを回してみると台形制御と3次関数接続の違いもモーターの軸の回転を見ているだけだとあまりわからない。定量的測定が必要。
注意すべきは、同じ時間内で動作を完了するには加速度のピークが台形制御よりも高くなり、逆に加速度の上限値を揃えた状態で比較すると動作時間が長くなる事。ピークの高さは
* 二次曲線で2倍
* 三次曲線で1.5倍
* 三角関数曲線で \(\pi/2\)倍
モーターの仕様では加速度の最大値が決まっていたりするので、これがボトルネックになると動作時間が長くなってしまう。しかし実際問題現在の回転数等に関わらず一定の加速度が上限になるというのも割合雑な取り決めのような気がするし、動かしてみて大丈夫ならOKというような世界なのかも知れない。
後、総移動距離が少なくて最大速度に到達する前に減速が始まるパターンの場合の計算が面倒。台形制御なら加速時の直線と減速時の直線のクロスポイントで切り替えるだけだが、S字制御でそれをやるとせっかくなだらかにした加速度に不連続点が出るため、最大加速度を下げてカーブを繋ぐ必要がある。
Posted by g200kg : 2018/03/29 10:51:02



