VSTiの作り方
8.おまけ (BLITのお話)
BLITって知ってますか? シンセを作ってる人じゃないとあまりなじみが無い言葉だとは思うのですが、時々ソフトシンセで、BLITを使ってます、とかいう売り文句があったりしますよね。ちょっとこのBLITについて書いてみたいと思います。
詳しくはこのあたりにあります
https://ccrma.stanford.edu/~stilti/papers/blit.pdf
後はTALさんが書いているこのページなんかは読みやすいです。
http://www.kunz.corrupt.ch/?DSP:Blit
BLIT は 「Band Limited Impulse Train」の略です。 Impulse Trainはインパルスがずらっと並んだ事を表しています。つまり、下の赤い線みたいにひげのようなパルスが一定間隔で並んだ波形です。Band Limited というのは帯域制限されているという事で、このインパルスが並んだ波形を理想的なローパスフィルターでナイキスト周波数より上をばっさりと切り落とした状態です。するとどうなるかというと、下の青い線の図みたいな波形になります。
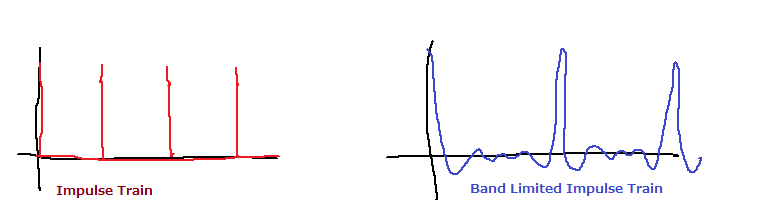
数式的には
y(n) = (M/P) * SincM ((M/P) * n)
ただし
SincM(x)= sin(PI * x) / (M * sin(PI * x / M) )
て感じで表されます。
もうちょっとまとめると
y(n) = sin( PI * M / P * n) / (sin(PI / P * n) * P)
ここで、Pは1周期のサンプル数。MはPを超えない奇数で、帯域制限の上限を表しています。つまりMが大きいほど青線のうねうねが細かくなって本来のインパルスの形に近づいて行きます。
で、これが何の役に立つのでしょうか?
ここで話変わってオシレーターの作り方
例えばのこぎり波を作りたいとします。出したい周波数とサンプリング周波数の比から1サンプルあたりの差分 delta を作って、
phase += delta
if(phase >=1.0)
phase -= 1.0
てやれば振幅が0.0 から 1.0 の範囲で変化するのこぎり波になりますが、実はこれだけだとエイリアスノイズが発生するという問題があります。これの何が悪いのさ、出したい理想波形上の点に一致してるでしょ、嫌なら後でフィルターでもかませば、て思うかも知れませんが、オシレーターの出力としてこういう波形を出した時点で駄目なんです。
例えばこの要領で矩形波を作ると、
if(phase >=0.5)
out=1.0
else
out=0.0
矩形波なんて0と1しかないんだからこんなんで良いんじゃね? と思いますが、44.1KHzのサンプリングレートで440Hzの音なら1周期が100.227ですから、100サンプルのサイクルと101サンプルのサイクルが周期的に混じったものになります、と言えば少なくともこれではまずいというのが直感的にわかりやすいですね。この周期のブレは音の濁りになり、これは後でフィルター掛けても既にノイズは折り返されて低い周波数になってますので取り除けません。
じゃあどうなんなきゃいけないのさ、と言うと、答えの1つが加算合成、アディティブシンセシスです。どんな波形でもサイン波を足していけば作れます、て言うのはフーリエ変換の説明の頭とかに出てきますけど、
sin(p) + sin(p*2)/2 + sin(p*3)/3 + sin(p*4)/4 +.....
て感じでナイキスト周波数以下の範囲で足して行けばエイリアスノイズのないのこぎり波が合成できます。こうやって加算合成で波形を作るのは DSF (Discrete-Summation Formulae) とも呼ばれます。 でもこれはさすがに計算が大変すぎます。1サンプル決めるのにどんだけ計算するんだよ、て感じですね。
て所で、BLITを使うわけです。エイリアスの発生しないBLIT波形にちょいと細工をしていろんな波形をつくってしまおうというもくろみですね。BLIT波形の性質は基本的にはインパルス列と同じようなもので、積分すると(積算してゆけば)段差が1の階段状の波形になるので、積算しながら1/Pを引く事でのこぎり波ができます。極性とかは後でなんとかしてください。
y(n+1) = y(n) + sin( PI * M / P * n) / (sin(PI / P * n) * P) - 1/P
て事ですね。sin()関数がいっぱいあったのがこれだと2つですみます。おー。
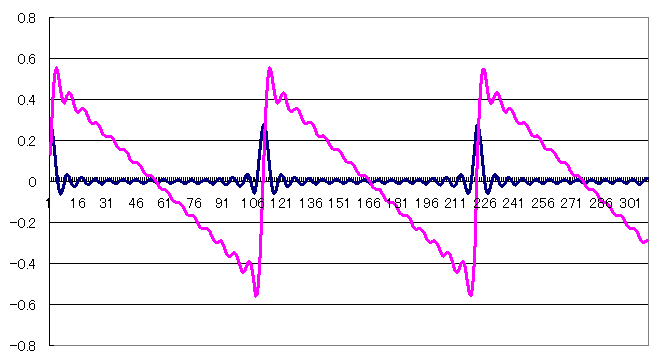
他のパターンとして、矩形波を作りたい場合はバイポーラBLITと言う波形を使います。バイポーラBLITというのは上下に順番にパルスが出るBLIT波形なんですが、実はBLITの式
y(n) = sin( PI * M / P * n) / (sin(PI / P * n) * P)
でMを偶数にするだけでできます。バイポーラBLITの積分は段差1を上がったり下がったりしますので、矩形波を作るのならこれを加算してゆくだけです。周波数は1/2になりますけど。
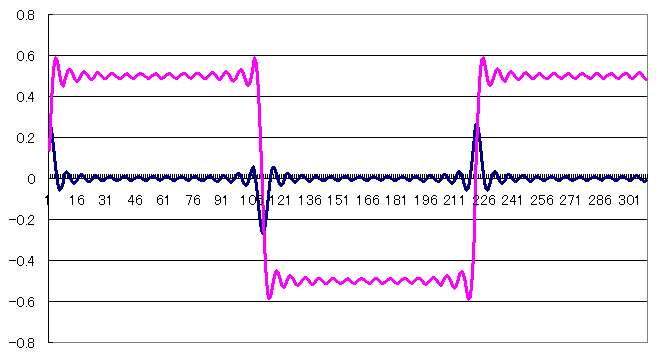
とまあ、これがBLIT方式による波形の発生の基本的な原理です。
しかしですね。2回とは言え1サンプル毎にsin()の計算が必要なんで、実際のシンセの実装としては、BLITを売り物にするんでなければ、あらかじめ作っておいた波形テーブルとかでやる方が一般的ですね。ただ、BLITもそうだけどナイキスト周波数ぎりぎりまで使ったエイリアスの出ない波形は出そうとしている周波数が変わると変わっちゃいますので、周波数範囲を幾つかに分けてテーブルを切り替えるとか色々このあたりはみなさん工夫しているようですよ。
まあ、ものが楽器ですのでエイリアスが全くない波形が唯一素晴らしいのか、という問題もありますし。どんなノイズが含まれているかも含めて、その楽器の音ですからね。



