簡単な式で波形生成してみる

2012/12/04 (2012年12月のアーカイブ)

簡単な式で波形生成してみる

この記事はWeb Music Developers JP のAdvent Calendar 2012用の記事です。
クリスマスまで日替わりのテーマで何か面白い記事が投稿される予定ですので、興味がありましたらどうぞ!
http://www.adventar.org/calendars/22

######

今回のテーマはシンセサイザーのオシレーターの実装です

シンセサイザーで音の元となる波形を生成するオシレーターをどうやって作るかは、それぞれに工夫を凝らす部分で、例えばBLITなんていう技術が使われたりもするのですが、多分一番多いのは波形テーブルを参照するやり方でしょう。多少メモリは使いますが、どんな波形でもテーブルさえ作ってしまえばあまり負荷もかからずに波形生成できますしね。

でも今回はもっとカジュアルに数式から波形生成する方法の一例を紹介します。なおこの方法はエイリアスノイズの対処が一切されていないので、そのまま出力する波形の品質としては今いちです。使いどころはちょっと限られるのですが、その代わりにとにかくシンプルで軽いです。それから多分ソースを見た人に「なんだこれ??」と思わせる効果がありそうです。

とりあえずソースをどうぞ。これだけで、鋸歯状波(SAWTOOTH) / 三角波(TRIANGLE) / 矩形波(SQUARE) / サイン波(SINE)の4種類の波形を生成する事ができます。


// 初期化
var phase=0;
var delta=freq/samplerate;
var x1,x2,y;

// 波形設定
function SetWaveForm(waveform) {
    switch(waveform) {
    case SAWTOOTH:
        x1=0; x2=2; y=2; z=0;
        break;
    case TRIANGLE:
        x1=0.5; x2=1.5; y=4; z=0;
        break;
    case SQUARE:
        x1=0.5; x2=1.5; y=100000; Z=0;
        break;
    case SINE:
        x1=0.5; x2=1.5; y=2*Math.PI; z=1/6.78;
        break;
    }
}

// 1サンプルの処理
function GetOutput() {
    if((phase+=delta)>=1.0)
        phase-=1.0;
    var t = ( Math.min( Math.max(phase ,x1 - phase), x2 - phase) - 0.5) * y;
    var out = t - t*t*t*z;
    if(out>1.0)
        out=1.0;
    if(out<-1.0)
        out=-1.0
    return out;
}

ポイントとしては波形にかかわらず単一の式で生成を行い、波形の切り替えは静的な係数が違うだけになっています。

初期化の後、SetWaveForm()で波形を設定します。各波形に応じて係数x1,x2,y,zの4つを設定するだけです。

その後は、サンプル毎にGetOutput()で出力値が計算されます。delta は周波数freqに対する1サンプルあたりの差分、phaseが0.0 ～ 1.0 の範囲で現在の位相をあらわしています。26行あたりで phase に delta を加算しつつ1.0を超えたら戻す処理をしていますね。

問題は28行目です。何をやってるのか非常にわかりにくいですが、まず、x1から下がる直線とx2から下がる直線の間に入るように折り返し、次に0.5を中心に取り直してyの倍率をかけています。SAWTOOTHとTRIANGLEの場合の折り返しの様子が下の図です。

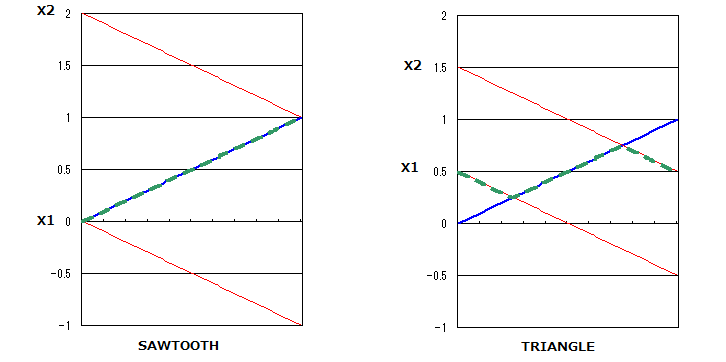
SAWTOOTHの場合は0.0-1.0の上昇する直線がそのまま出力されますが、TRIANGLEの場合は折り返されて三角波状になっています。どちらも0.5が中心ですが、TRIANGLEは折り返された分振幅が小さくなりますのでyの係数で調整します。

SQUAREの場合はと言うと折り返しに関してはTRIANGLEと同じですが、倍率yが100000と大きな値になっています。つまり28行目の所では超巨大三角波ですが、出力は30行目あたりで-1.0 ～ 1.0 の範囲に制限されていますので、クリップして結果として(ほぼ)矩形波になります。

SINEの場合はどうでしょうか? 倍率は違いますが基本は三角波に近く、今まで使ってなかったzの係数が設定されて29行目の計算が生きてきます。これは簡単に言えば3次関数での近似で三角波の頭を潰す形でサイン波に近い所に無理やり合わせているという処理です。変換の元になる値は倍率 2*PI なので0.0 ～ 0.25 の振幅を 0 ～ PI/2 に変換しています。

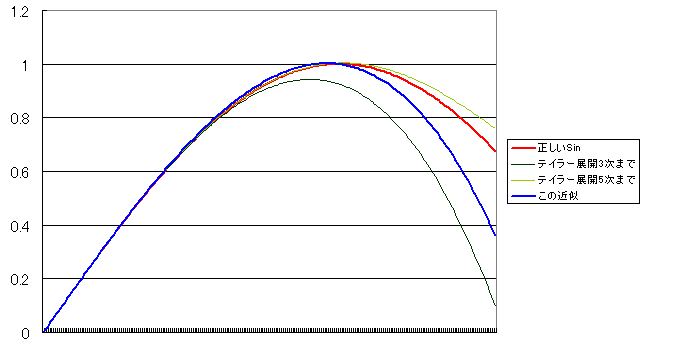
Sin()のテイラー展開は下の式のような感じですので、3乗の項だけ計算しているのに近いですね。ただし、3乗の項の分母は6ではなく、以降を省略した誤差の埋め合わせのため6.78になっています。これは波形の頂点が不連続にならないようにするためのexperimentalな値です。


sin(x) = x - pow(x,3)/(3*2) + pow(x,5)/(5*4*3*2) - pow(x,7)/(7*6*5*4*3*2) + ....

この近似は実は結構歪んでいるので精度を求めるのなら、テイラー展開の5次の項まで計算してやればかなり良くなるんですが、あくまでシンプルでパフォーマンス優先としています。

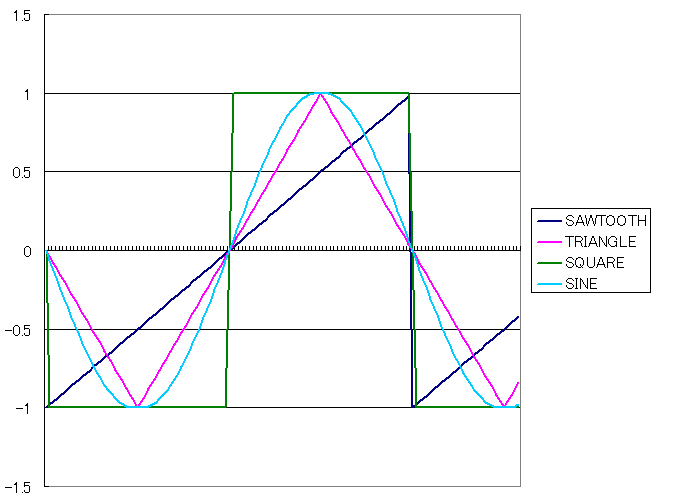
という事で、波形生成の1方法のご紹介でした。エイリアスとかがあまり問題にならないLFOなんかにいかがですか? この方式で作った各波形は下の図のような感じになります。

Posted by g200kg : 2012/12/04 00:28:00

最近の記事

関連記事

2012/12/04 (2012年12月のアーカイブ)